Skip to main content
Contents Index Calc Dark Mode Prev Up Next \(\newcommand{\R}{\mathbb{R}}
\newcommand{\va}{\vec{a}}
\newcommand{\vb}{\vec{b}}
\newcommand{\vc}{\vec{c}}
\newcommand{\vC}{\vec{C}}
\newcommand{\vd}{\vec{d}}
\newcommand{\ve}{\vec{e}}
\newcommand{\cursedihat}{\hat{\dot{i}}}
\newcommand{\vi}{\hat{\imath}}
\newcommand{\vj}{\hat{\jmath}}
\newcommand{\vk}{\hat{k}}
\newcommand{\vn}{\vec{n}}
\newcommand{\vm}{\vec{m}}
\newcommand{\vr}{\vec{r}}
\newcommand{\vs}{\vec{s}}
\newcommand{\vu}{\vec{u}}
\newcommand{\vv}{\vec{v}}
\newcommand{\vw}{\vec{w}}
\newcommand{\vx}{\vec{x}}
\newcommand{\vy}{\vec{y}}
\newcommand{\vz}{\vec{z}}
\newcommand{\vzero}{\vec{0}}
\newcommand{\vF}{\vec{F}}
\newcommand{\vG}{\vec{G}}
\newcommand{\vH}{\vec{H}}
\newcommand{\vR}{\vec{R}}
\newcommand{\vT}{\vec{T}}
\newcommand{\vN}{\vec{N}}
\newcommand{\vL}{\vec{L}}
\newcommand{\vB}{\vec{B}}
\newcommand{\vS}{\vec{S}}
\newcommand{\proj}{\text{proj}}
\newcommand{\comp}{\text{comp}}
\newcommand{\nin}{}
\newcommand{\vecmag}[1]{\left\lVert #1\right\rVert}
\newcommand{\grad}{\nabla}
\newcommand\restrict[1]{\raise-.5ex\hbox{$\Big|$}_{#1}}
\DeclareMathOperator{\curl}{curl}
\DeclareMathOperator{\divg}{div}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
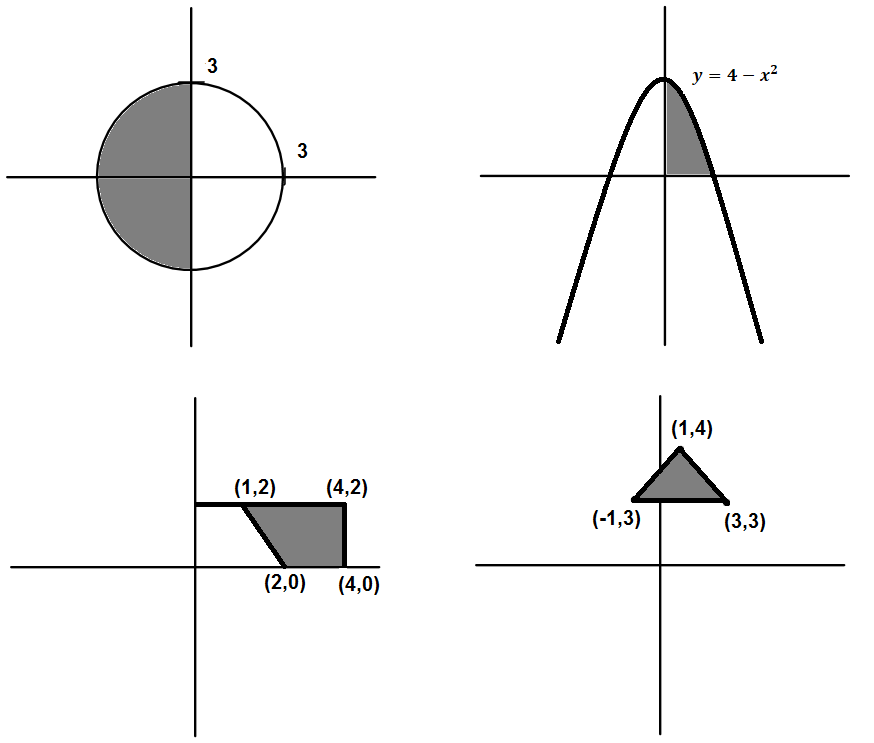
Activity 12.3.4 .
(a) For each region, state whether the region is vertically simple, horizontally simple, both, or neither. State the appropriate inequalities to justify when each region is vertically simple or horizontally simple.
Figure 12.3.17. Four Regions of the \(xy\) -plane
(b)
Which of the following expressions do not make sense as an iterated integral used to compute a double integral? If the iterated integral does not make sense, explain your reasoning in a couple of sentences. If the iterated integral does make sense, draw a plot of the region of integration.
\begin{equation*}
\int_0^1 \int_1^x f(x,y) \; dy \; dx
\end{equation*}
\begin{equation*}
\int_0^1 \int_1^y f(x,y) \; dy \; dx
\end{equation*}
\begin{equation*}
\int_0^1 \int_x^y f(x,y) \; dy \; dx
\end{equation*}
\begin{equation*}
\int_0^1 \int_x^1 f(x,y) \; dy \; dx
\end{equation*}